Links:

Electrical Conductivity of Conjugated Polymers

Polymers have long been known as insulating materials and are often used to insulate cables and electrical devices. However, there are also a number of polymers that are electrically conductive. The electrical conductivity of these polymers is based on the presence of conjugated double bonds along the polymer backbone. Conjugation means that the polymer backbone consists of alternating single and double bonds. The strong chemical bonds between the carbon atoms are the so-called localized σ bonds, whereas the double bonds provide weaker and less strongly localized π bonds. However, the conductivity of these polymers is rather low. Only when an electron is removed from the valence band by oxidation (p-doping) or added to the conducting band by reduction (n-doping) does the polymer become highly conductive. Through such a doping process, charge defects (polaron, bipolaron and soliton) are created that can travel through the backbone of the polymer, or to be more specific, through the conduction band.

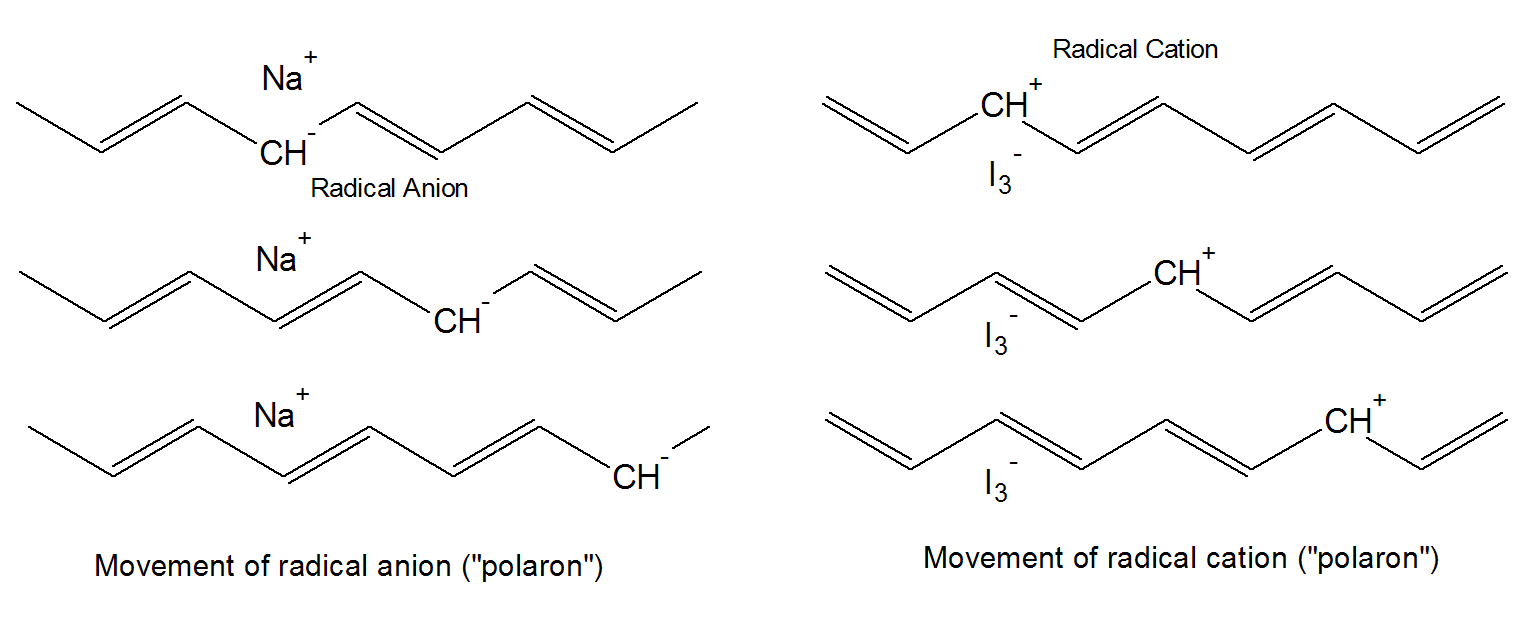
The radical cations / anions, also called polarons1,  that form during doping, are partially localized mainly because of Coulomb attraction to its counterion which has normally a mucher lower mobility. Thus, it is not the counter ion, such as I3- or Na+, but the charges on the polymer backbone that are the mobile charge carriers. Because of the strong interaction with the counterion, a relative high concentration of dopant (about 10 percent) is required to allow the polarons to move in the field of surrounding counterions.

Both the charge transport processes and their relative importance are still not fully understood.

The conductivity2 of a material depends on both the density of charge carriers (number of charges per unit volume) and how fast they can move in the material, to be more specific, on their mobility μ.

A simple relationship between mobility of the charge carriers and the electrical conductivity σ exist. If μe and μp are the mobilities of negative charges (electrons) and positive charges (these are missing electrons called holes) then each of these charge carriers will move with the velocity vector μeE and μpE in the electric field E. The total current density is then

σ = e (ne μe + np μp)

where e is the elementary charge, and ne and np are the number density (concentration) of negative charges (electrons) and positive charges (holes).

The conductivity strongly depends on the temperature. For metals, it decreases with increasing temperature, whereas for semi-conductors like conducting polymers it increases.

Notes

  1. A polaron is a quasi particle that exists in condensed matter. It consists of an electron and the (lattice) distortion field that it induces in the surrounding matter. This interaction is of fundamental importance in condensed-matter physics.

  2. The conductivity of any material is given by Ohm’s law: U = R · I, where I is the current flowing through the resistor, in this case the conductive polymer, and U is the drop in potential across it. The proportionality constant R is called the “resistance”.  In an Ohmic material, the resistance is proportional to the length L of the conductor and inversely proportional to its cross-section A:

    R = ρ · L / A = L / (Aσ),

    where ρ is the resistivity in Ωm, and its inverse σ is the conductivity of the material measured in S/m (Siemens per meter).
    Not all materials obey Ohm’s law. Gas discharges, semiconductors and one-dimensional conductors like a single conjugated polyene chain generally deviate from Ohm’s law.

  • Summary

    Intrinsically conducting polymers (ICPs) have been the subject of intense research. These polymers have unique electrical properties. Their electrical conductivity is based on conjugated double bonds along the polymer backbone.

  • Conjugation alone results in low electrical conductivity. In addition, the polymer has to be doped with charge carriers, which provide "holes” (orbitals with a missing electron). These "holes" can be filled by electrons of neighboring carbon atoms, creating new holes and so on, thus, allowing the flow of charges over long distances.

  • Band Theory

    According to the band theory of conductors, the electrical properties of a semi-conductor with a direct gap depend on its electronic structure.

  • It is assumed that the electrons move within discrete energy states called bands. The highest occupied band is called the valence band, and the lowest unoccupied band is the conduction band.

  • Because of partially filled energy bands, metals have high conductivities, whereas the energy bands of insulators and semiconductors are either completely filled or completely empty.

  • For example, all conventional polymers have completely filled valence bands but empty conduction bands, which are separated from each other by a wide energy gap, whereas conductive polymers have relative narrow band gaps.

  • Doping can change the band structure by either removing electrons from the valence band (p-doping) or by adding electrons to the conduction band (n-doping).